An Illustrated Theory of Numbers
Martin H. Weissman
Published by the American Mathematical Society
2018 Prose awards, Honorable Mention!

Published by the American Mathematical Society
2018 Prose awards, Honorable Mention!
The American Mathematical Society (AMS) provides member discounts, frequent sales, and reviewer/desk copies for faculty teaching number theory.
But if you prefer, you can also purchase from Amazon.
An Illustrated Theory of Numbers gives a comprehensive introduction to number theory, with complete proofs, worked examples, and exercises. Its exposition reflects the most recent scholarship in mathematics and its history. For the latest updates, follow us on Facebook.
See the AMS book page for editorial reviews. For published reviews and testimonials, click below.
Becaus misstkes happpen,
Written and refined over 10 years of teaching undergraduate students, K-12 teachers, and talented high-school students. I have endeavored to give clear proofs with almost 500 crisp illustrations, concise exposition and examples, and scholarship reflecting the state of the art in mathematics and its history.
Examination and desk copies available from the AMS.
Sample syllabi, quizzes, student project ideas, and more. Eventually I plan to provide resources for teaching number theory here. If you're teaching computational aspects of number theory, you may be interested in the Python programming notebooks below. If you would like to share your teaching materials, feel free to send me a note at weissman AT ucsc DOT edu.
Have you used this book in the classroom? I would love to hear about your experience. Send me a note at weissman AT ucsc DOT edu, if you are planning to teach or have taught with An Illustrated Theory of Numbers.
See the AMS book page for editorial reviews. For published reviews and testimonials, click below.
Learning number theory?
Reading mathematics is a type of close reading that takes patience and practice. Here is some good advice, courtesy of Ashley Reiter and published by the MAA. Read An Illustrated Theory of Numbers slowly, with pen and paper nearby. Dwell on the pictures, the definitions, the theorems, and the proofs. Give yourself 30 minutes per page. If you get stuck, sleep on it... and be confident that understanding will come eventually. The best way to remember something is to know why it is true.
Supplemental readings about number theory, and mathematics more broadly. Great books and websites. Useful links for undergraduates interested in mathematics. I will curate some of the best resources. Coming soon...
If you can program, you have a powerful way to solve problems, to explore applications of number theory to cryptography, and to strengthen your understanding of mathematics. Programming doesn't hurt when you're applying for jobs either. So learn to program! I've put together an introduction to programming that's designed to complement the book.
Learn Python alongside number theory
Python is a great language for newcomers to programming, and is widely used in industry and scientific research. Python is the central language in which SAGE is built and used, for those pursuing research in number theory. Programming can strengthen your understanding of number theory, and enables the study of modern cryptography.
We recommend installing Python (3.x) through the Anaconda distribution, since it is free and it works across platforms (Mac OS, Windows, Linux) to give a uniform experience across the classroom. This includes everything you'll need for running the instructional Python notebooks, plus much more.
A series of instructional Python notebooks, to take you from absolute programming beginner to the implementation of algorithms in number theory, from the sieve of Eratosthenes, Miller-Rabin primality testing, the RSA cryptosystem, and more. Now available for Python 2 and Python 3!
Art prints, adapted from images in the book. Suitable for home, office, or classroom. Each is created as a vector graphic (PDF), and converted at high resolution for sharp text and lines at large sizes. All posters are printed on acid-free paper with archival inks to last 75 years, with 30-day money-back guarantee. All posters and other items sold, printed, and shipped by Fine Art America.
Purchase from Fine Art America.
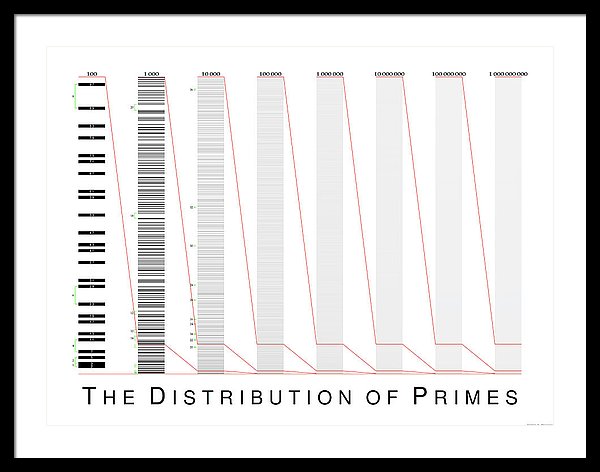
The prime numbers between 1 and 1 billion are visualized at successively larger scales. The left column displays the primes from 1 to 100 as individuals. The small-scale irregularities smooth out as one considers primes between 1 and 1000, 1 and 10000, etc. The rightmost column displays the primes from 1 to 1 billion as an almost uniform shade of gray. The amount of black ink is precisely the density of primes, e.g., if 5% of numbers are prime within a range, that range is shaded by black ink at a density of 5%. Created as a vector graphic, and printed at high-resolution for crisp lines at large size. A size of 20" by 15" looks good on the wall.

Purchase from Fine Art America.
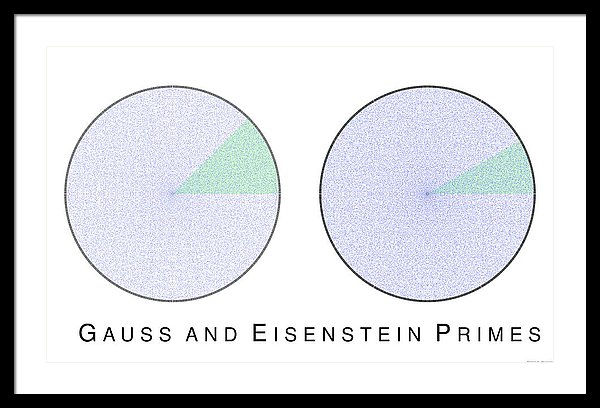
Within the Gaussian integers Z[i] and Eisenstein integers Z[w] (w a primitive cube root of unity), the Gaussian and Eisenstein prime numbers are displayed. Almost 100,000 primes are displayed in each circle, and the "prime angles" are marked with ticks around the circumference. The green pie-pieces are fundamental domains, breaking the symmetries given by the Gaussian and Eisenstein units, together with complex conjugation. A size of 24" by 15" looks good on the wall.


Purchase from Fine Art America.
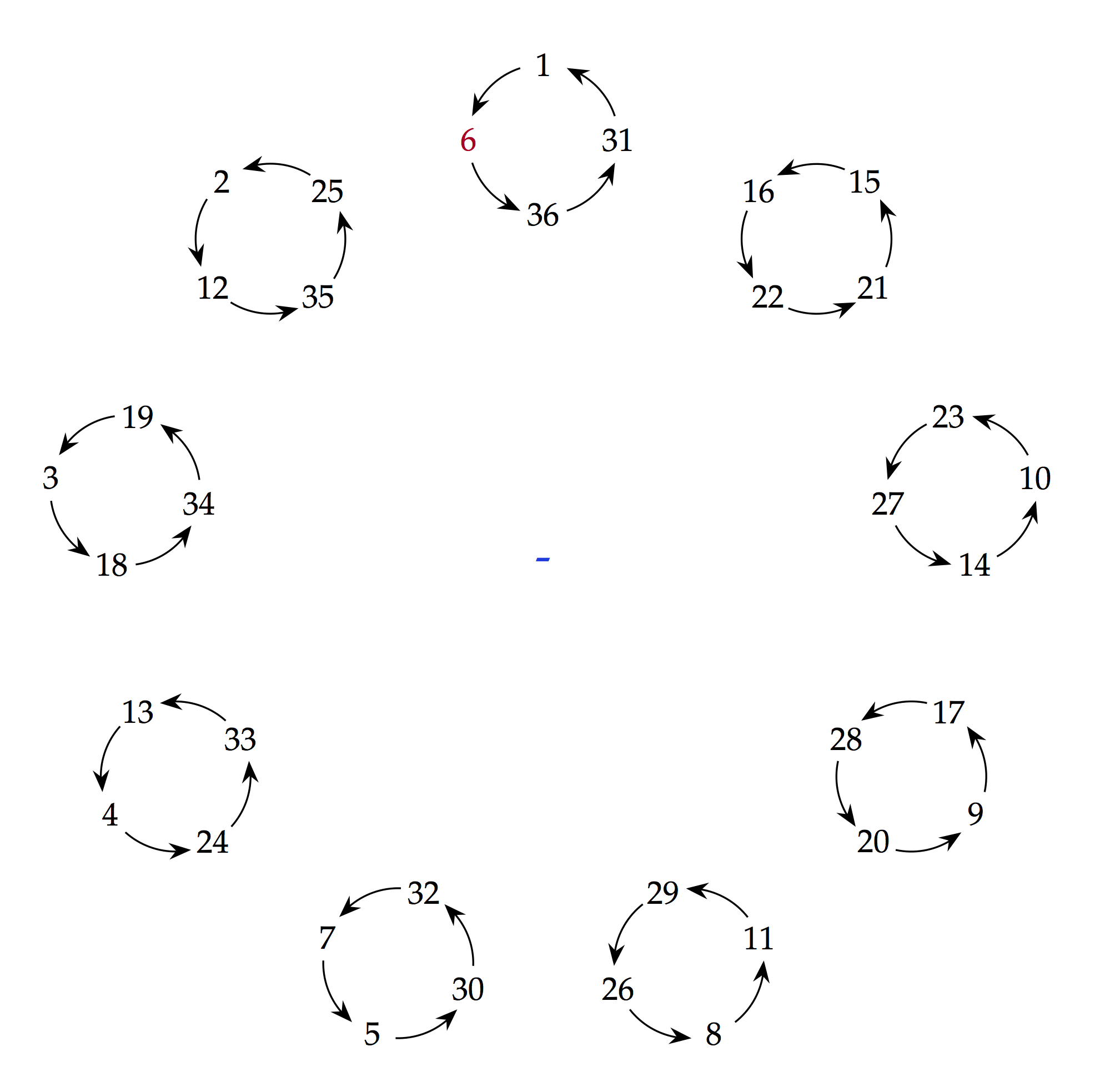
The numbers 1 through 36 are arranged in 36 different diagrams, displaying the dynamics of multiplication modulo 37. Primitive roots modulo 37 appear as large circles. Each cycle is labeled by a sign (+/-) according to its sign as a permutation. This illustrates Zolotarev's Lemma, connecting the sign of the "multiplication by a mod p" permutation to the Legendre symbol. Students will find their own patterns. Who knew that a cyclic group could be so pretty? A size of 22.75" by 24" looks good on the wall, though bigger might be better if you want to see the numbers from afar.
Published by the American Mathematical Society.
Published August, 2017
(Website design by Martin H. Weissman. Contact at weissman AT ucsc DOT edu)